Vector Calculus

Vectors in Euclidean Space

1.1 Introduction

In single-variable calculus, the functions that one encounters are functions of a variable (usually x or t) that varies over some subset of the real number line (which we denote by R). For such a function, say, y = f (x), the graph of the function f consists of the points (x, y) = (x, f (x)). These points lie in the Euclidean plane, which, in the Cartesian or rectangular coordinate system, consists of all ordered pairs of real numbers (a, b). We use the word “Euclidean” to denote a system in which all the usual rules of Euclidean geometry hold. We denote the Euclidean plane by R2; the “2” represents the number of dimensions of the plane. The Euclidean plane has two perpendicular coordinate axes: the x-axis and the y-axis.

In vector (or multivariable) calculus, we will deal with functions of two or three variables (usually x, y or x, y, z, respectively). The graph of a function of two variables, say, z = f (x, y), lies in Euclidean space, which in the Cartesian coordinate system consists of all ordered triples of real numbers (a, b, c). Since Euclidean space is 3-dimensional, we denote it by R3. The graph of f consists of the points (x, y, z) = (x, y, f (x, y)). The 3-dimensional coordinate system of Euclidean space can be represented on a flat surface, such as this page or a black- board, only by giving the illusion of three dimensions, in the manner shown in Figure 1.1.1. Euclidean space has three mutually perpendicular coordinate axes (x, y and z), and three mutually perpendicular coordinate planes: the xy-plane, yz-plane and xz-plane (see Figure 1.1.2).

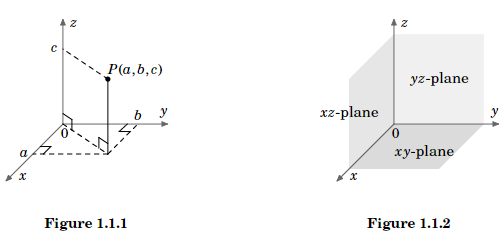
The coordinate system shown in Figure 1.1.1 is known as a right-handed coordinate system, because it is possible, using the right hand, to point the index finger in the positive direction of the x-axis, the middle finger in the positive direction of the y-axis, and the thumb in the positive direction of the z-axis, as in Figure 1.1.3.

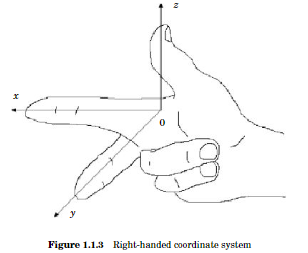
An equivalent way of defining a right-handed system is if you can point your thumb up- wards in the positive z-axis direction while using the remaining four fingers to rotate the x-axis towards the y-axis. Doing the same thing with the left hand is what defines a left- handed coordinate system. Notice that switching the x– and y-axes in a right-handed system results in a left-handed system, and that rotating either type of system does not change its “handedness”. Throughout the book we will use a right-handed system.

For functions of three variables, the graphs exist in 4-dimensional space (i.e. R4), which we can not see in our 3-dimensional space, let alone simulate in 2-dimensional space. So we can only think of 4-dimensional space abstractly. For an entertaining discussion of this subject, see the book by ABBOTT.1

So far, we have discussed the position of an object in 2-dimensional or 3-dimensional space. But what about something such as the velocity of the object, or its acceleration? Or the gravitational force acting on the object? These phenomena all seem to involve motion and direction in some way. This is where the idea of a vector comes in.