The Zakon Series on Mathematical Analysis – Mathematical Analysis Volume II

Chapter 6 – Differentiation on  and Other Normed Linear Spaces

1. Directional and Partial Derivatives

In Chapter 5 we considered functions f : E1 → E of one real variable.

Now we take up functions f : E′ → E where both E′ and E are normed spaces.

The scalar field of both is always assumed the same: E1 or C (the complex field). The case E = E∗ is excluded here; thus all is assumed finite.

We mostly use arrowed letters for vectors in the domain space E′, and nonarrowed letters for those in E and for scalars.

As before, we adopt the convention that f is defined on all of E′, with f(~x) = 0 if not defined otherwise.

Note that, if ~p ∈ E′, one can express any point as

with t ∈ E1 and ~u a unit vector. For if set

and if  set t = 0, and any ~u will do. We often use the notation

First of all, we generalize Definition 1 in Chapter 5,

Definition 1

Given , we define the directional derivative of f along ~u (or ~u-directed derivative of f) at ~p by

if this limit exists in E (finite). We also define the ~u-directed derived function,

as follows. For any

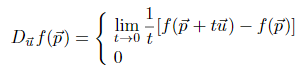  if this limit exists, otherwise.

Thus is always defined, but the name derivative is used only if the limit (1) exists (finite). If it exists for each in a set B ⊆ E′, we call (in classical notation ∂f/∂~u) the ~u-directed derivative of f on B.

Note that, as t → 0, tends to ~p over the line Thus can be treated as a relative limit over that line. Observe that it depends on both the direction and the length of . Indeed, we have the following result.