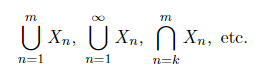The Zakon Series on Mathematical Analysis – Mathematical Analysis Volume I

Chapter 1 – Set Theory

1–3. Sets and Operations on Sets. Quantifiers

A set is a collection of objects of any specified kind. Sets are usually denoted by capitals. The objects belonging to a set are called its elements or members. We write x ∈ A if x is a member of A, and xA if it is not.

A = {a, b, c, . . . } means that A consists of the elements a, b, c, . . . . In particular, A = {a, b} consists of a and b; A = {p} consists of p alone. The empty or void set, ∅, has no elements. Equality (=) means logical identity .

If all members of A are also in B, we call A a subset of B (and B a superset of A), and write A ⊆ B or B ⊇ A. It is an axiom that the sets A and B are equal (A = B) if they have the same members, i.e., A ⊆ B and B ⊆ A.

If, however, A ⊆ B but B A (i.e., B has some elements not in A), we call A a proper subset of B and write A ⊂ B or B ⊃ A. “⊆” is called the inclusion relation.

Set equality is not affected by the order in which elements appear. Thus {a, b} = {b, a}. Not so for ordered pairs (a, b).1 For such pairs,
(a, b) = (x, y) iff2 a = x and b = y,
but not if a = y and b = x. Similarly, for ordered n-tuples,

We write {x | P (x)} for “the set of all x satisfying the condition P (x).” Similarly, {(x, y) | P (x, y)} is the set of all ordered pairs for which P (x, y) holds; {x ∈ A | P (x)} is the set of those x in A for which P (x) is true.

For any sets A and B, we define their union A ∪ B, intersection A ∩ B, difference A−B, and Cartesian product (or cross product) A×B, as follows:

A ∪B is the set of all members of A and B taken together :
{x | x ∈ A or x ∈ B}.3

A ∩B is the set of all common elements of A and B:
{x ∈ A | x ∈ B}.

A−B consists of those x ∈ A that are not in B:
{x ∈ A | x B}.

A×B is the set of all ordered pairs (x, y), with x ∈ A and y ∈ B:
{(x, y) | x ∈ A, y ∈ B}.

Similarly, A1×A2×· · ·×An is the set of all ordered n-tuples (x1, . . . , xn) such that xk ∈ Ak, k = 1, 2, . . . , n. We write An for A×A× · · · ×A (n factors).

A and B are said to be disjoint iff A ∩ B = ∅ (no common elements). Otherwise, we say that A meets B (A ∩ B∅). Usually all sets involved are subsets of a “master set” S, called the space. Then we write −X for S −X, and call −X the complement of X (in S). Various other notations are likewise in use.

Examples.

Let A = {1, 2, 3}, B = {2, 4}. Then
A ∪B = {1, 2, 3, 4}, A ∩B = {2}, A−B = {1, 3},
A×B = {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}.

If N is the set of all naturals (positive integers), we could also write
A = {x ∈ N | x < 4}.

Theorem 1.

(a) A ∪A = A; A ∩A = A;
(b) A ∪B = B ∪A, A ∩B = B ∩ A;
(c) (A ∪B) ∪ C = A ∪ (B ∪ C); (A ∩B) ∩ C = A ∩ (B ∩ C);
(d) (A ∪B) ∩ C = (A ∩ C) ∪ (B ∩ C);
(e) (A ∩B) ∪ C = (A ∪ C) ∩ (B ∪ C).

The proof of (d) is sketched in Problem 1. The rest is left to the reader.

Because of (c), we may omit brackets in A∪B ∪C and A∩B ∩C; similarly for four or more sets. More generally, we may consider whole families of sets, i.e., collections of many (possibly infinitely many) sets. IfM is such a family, we define its union, ⋃M, to be the set of all elements x, each belonging to at least one set of the family. The intersection of M, denoted ⋂M, consists of those x that belong to all sets of the family simultaneously . Instead, we also write

Often we can number the sets of a given family:

A1, A2, . . . , An, . . . .

More generally, we may denote all sets of a familyM by some letter (say, X) with indices i attached to it (the indices may, but need not , be numbers). The familyM then is denoted by {Xi} or {Xi | i ∈ I}, where i is a variable index ranging over a suitable set I of indices (“index notation”). In this case, the union and intersection ofM are denoted by such symbols as

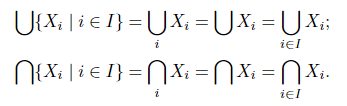
If the indices are integers, we may write m ⋃