Tea Time Numerical Analysis – Experiences in Mathematics

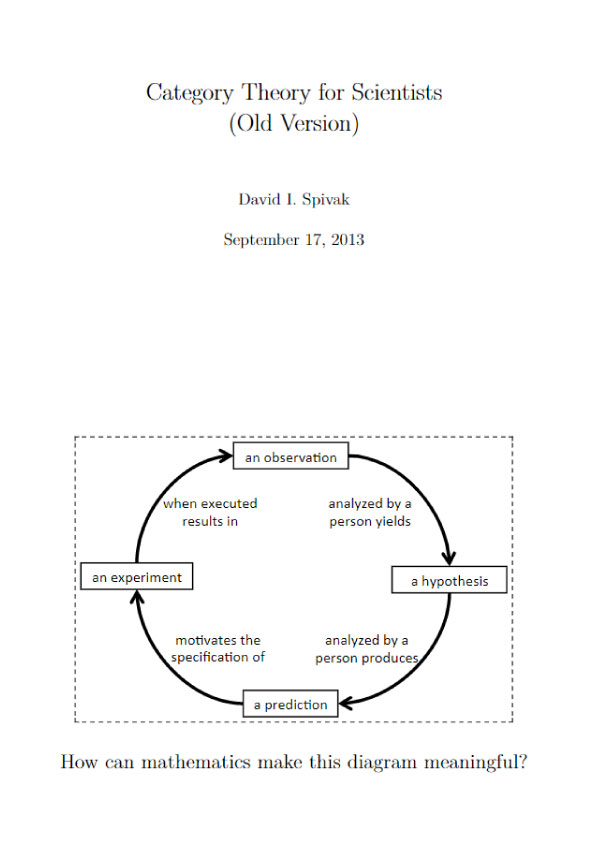
Chapter 1 – Preliminaries

1.1 Accuracy Measuring Error 

Numerical methods are designed to approximate one thing or another. Sometimes roots, sometimes derivatives or definite integrals, or curves, or solutions of differential equations. As numerical methods produce only approximations to these things, it is important to have some idea how accurate they are. Sometimes accuracy comes down to careful algebraic analysis—sometimes careful analysis of the calculus, and often careful analysis of Taylor polynomials. But before we can tackle those details, we should discuss just how error and, therefore, accuracy are measured.

There are two basic measurements of accuracy: absolute error and relative error. Suppose that p is the value we are approximating, and p̃ is an approximation of p. Then p̃ misses the mark by exactly the quantity p̃− p, the so-called error. Of course, p̃ − p will be negative when p̃ misses low. That is, when the approximation p̃ is less than the exact value p. On the other hand, p̃ − p will be positive when p̃ misses high. But generally, we are not concerned with whether our approximation is too high or too low. We just want to know how far off it is. Thus, we most often talk about the absolute error, |p̃ − p|. You might recognize the expression |p̃ − p| as the distance between p̃ and p, and that’s not a bad way to think about absolute error.

The absolute error in approximating p = π by the rational number . The absolute error in approximating π5 by the rational number 16525/54 is | 16525 /54 − π5| ≈ 0.00116. The absolute errors in these two approximations are nearly equal. To make the point more transparent, π ≈ 3.14159 and 22 7 ≈ 3.14285, while π5 ≈ 306.01968 and 16525 54 ≈ 306.01851. Each approximation begins to differ from its respective exact value in the thousandths place. And each is off by only 1 in the thousandths place.

But there is something more going on here. π is near 3 while π5 is near 300. To approximate π accurate to the nearest one hundredth requires the approximation to agree with the exact value in only 3 place values—the ones, tenths, and hundredths. To approximate π5 accurate to the nearest one hundredth requires the approximation to agree with the exact value in 5 place values—the hundreds, tens, ones, tenths, and hundredths. To use more scientific language, we say that 22/7 approximates π accurate to 3 significant digits while 16525 54 approximates π5 accurate to 5 significant digits. Therein lies the essence of relative errors—weighing the absolute error against the magnitude of the number being approximated. This is done by computing the ratio of the error to the exact value. Hence, the relative error in approximating π by 22/7 is 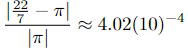while the relative error in approximating π5 by 16525/54 is 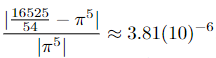. The relative errors differ by a factor of about 100 (equivalent to about two significant digits of accuracy) even though the absolute errors are nearly equal. In general, the relative error in approximating p by p̃ is given by .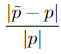