Principles of Programming Languages

Chapter 2 – Operational Semantics

2.1 A First Look at Operational Semantics

The syntax of a programming language is the set of rules governing the formation of expressions in the language. The semantics of a programming language is the meaning of those expressions.

There are several forms of language semantics. Axiomatic semantics is a set of axiomatic truths in a programming language. Denotational semantics involves modeling programs as static mathematical objects, namely as set-theoretic functions with specific properties. We, however, will focus on a form of semantics called operational semantics.

An operational semantics is a mathematical model of programming language execution. It is, in essence, an interpreter defined mathematically. However, an operational semantics is more precise than an interpreter because it is defined mathematically, and not based on the meaning of the programming language in which the interpreter is written. This might sound sound like a pedantic distinction, but interpreters interpret e.g. a languages if statements with the if statement of the language the interpreter is written in, etc, this is in some sense a circular definition of if. Formally, we can define operational semantics as follows.

Definition 2.1 (Operational Semantics). An operational semantics for a programming language is a mathematical definition of its computation relation, e⇒ v, where e is a program in the language.

e ⇒ v is mathematically a 2-place relation between expressions of the language, e, and values of the language, v. Integers and booleans are values. Functions are also values because they don’t compute to anything. e and v are metavariables, meaning they denote an arbitrary expression or value, and should not be confused with the (regular) variables that are part of programs.

An operational semantics for a programming language is a means for understanding in precise detail the meaning of an expression in the language. It is the formal specification of the language that is used when writing compilers and interpreters, and it allows us to rigorously verify things about the language.

2.2 BNF grammars and Syntax

Before getting into meaning we need to take a step back and first precisely define language syntax. This is done with formal grammars. Backus-Naur Form (BNF) is a standard grammar formalism for defining language syntax. You could well be familiar with BNF since it is often taught in introductory courses, but if not we provide a brief overview. All BNF grammars comprise terminals, non-terminals (aka syntactic categories), and production rules. Terminals are traditionally identified using lower-case letters; non-terminals are identified using upper-case letters. Production rules describe how non-terminals are defined. The general form of production rules is:

〈nonterminal〉 ::= 〈form 1〉 | · · · | 〈form n〉

where each “form” above describes a particular language form – that is, a string of terminals and non-terminals. A term in the language is a string of terminals which matches the description of one of these rules (traditionally the first).

For example, consider the language Sheep. Let {S} be the set of non-terminals, {a, b} be the set of terminals, and the grammar definition be:

S ::= b | Sa

Note that this is a recursive definition. Examples of terms in Sheep are

b, ba, baa, baaa, baaaa, . . .

That is, any string starting with the character b and followed by zero or more a characters is a term in Sheep. The following are examples that are not terms in SHEEP:

• a: Terms in Sheep must start with a b.
• bbaaa: Sheep does not allow multiple b characters in a term.
• baah: h is not a terminal in Sheep.
• Saaa: S is a non-terminal in Sheep. Terms may not contain non-terminals.

Another way of expressing a grammar is by the use of a syntax diagram. Syntax diagrams describe the grammar visually rather than in a textual form. For example, the following is a syntax diagram for the language Sheep:

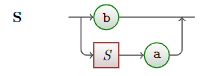
The above syntax diagram describes all terms of the Sheep language. To generate a form of S, one starts at the left side of the diagram and moves until one reaches the right. The rectangular nodes represent non-terminals while the rounded nodes represent terminals. Upon reaching a non-terminal node, one must construct a term using that non-terminal to proceed.

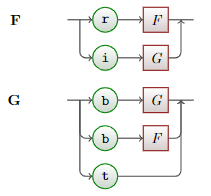
As another example, consider the language Frog. Let {F,G} be the set of non-terminals, {r, i, b, t} be the set of terminals, and the grammar definition be:

F ::= rF | iG
G ::= bG | bF | t

Note that this is a mutually recursive definition. Note also that each production rule defines a syntactic category. Terms in FROG include:

ibit, ribbit, ribibibbbit . . .

The following terms are not terms in Frog:

• rbt: When a term in Frog starts with r, the following non-terminal is F . The non-terminal F may only be exapnded into rF or iG, neither of which start with b. Thus, no string starting with rb is a term in Frog.
• rabbit: a is not a terminal in Frog.
• rrrrrrF : F is a non-terminal in Frog; terms may not contain non-terminals.
• bit: The only forms starting with b appear as part of the definition of G. As F is the first non-terminal defined, terms in Frog must match F (which does not have any forms starting with b).

The following syntax diagram describes Frog: