Linear Algebra – Jim Hefferon

Answer To Exercise

Chapter One – Linear Systems

I Solving Linear Systems

Systems of linear equations are common in science and mathematics. These two examples from high school science [Onan] give a sense of how they arise.

The first example is from Statics. Suppose that we have three objects, we know that one has a mass of 2 kg, and we want to find the two unknown masses. Experimentation with a meter stick produces these two balances.

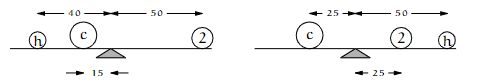
For the masses to balance we must have that the sum of moments on the left equals the sum of moments on the right, where the moment of an object is its mass times its distance from the balance point. That gives a system of two linear equations.

40h+ 15c = 100
25c = 50+ 50h

The second example is from Chemistry. We can mix, under controlled conditions, toluene and nitric acid HNO3 to produce trinitrotoluene along with the byproduct water (conditions have to be very well controlled— trinitrotoluene is better known as TNT). In what proportion should we mix them? The number of atoms of each element present before the reaction

must equal the number present afterward. Applying that in turn to the elements C, H, N, and O gives this system.

7x = 7z
8x+ 1y = 5z+ 2w
1y = 3z
3y = 6z+ 1w

Both examples come down to solving a system of equations. In each system, the equations involve only the first power of each variable. This chapter shows how to solve any such system of equations.

I.1 Gauss’s Method

1.1 Definition A linear combination of x1, . . . , xn has the form

a1x1 + a2x2 + a3x3 + · · ·+ anxn

where the numbers a1, . . . , an ∈ R are the combination’s coefficients . A linear equation in the variables x1, . . . , xn has the form a1x1 + a2x2 + a3x3 + · · ·+ anxn = d where d ∈ R is the constant .

An n-tuple (s1, s2, . . . , sn) ∈ Rn is a solution of, or satisfies, that equation if substituting the numbers s1, . . . , sn for the variables gives a true statement: a1s1 + a2s2 + · · ·+ ansn = d. A system of linear equations

a1,1×1 + a1,2×2 + · · ·+ a1,nxn = d1
a2,1×1 + a2,2×2 + · · ·+ a2,nxn = d2
…
am,1×1 + am,2×2 + · · ·+ am,nxn = dm

has the solution (s1, s2, . . . , sn) if that n-tuple is a solution of all of the equations.

1.2 Example The combination 3×1 + 2×2 of x1 and x2 is linear. The combination is not a linear function of x1 and x2, nor is 3×1 + 2 sin(x2).

We usually take x1, . . . , xn to be unequal to each other because in a sum with repeats we can rearrange to make the elements unique, as with 2x+ 3y+ 4x = 6x+ 3y. We sometimes include terms with a zero coefficient, as in x− 2y+ 0z, and at other times omit them, depending on what is convenient.

1.3 Example The ordered pair (−1, 5) is a solution of this system. 3×1 + 2×2 = 7 −x1 + x2 = 6 In contrast, (5,−1) is not a solution.

Finding the set of all solutions is solving the system. We don’t need guesswork or good luck; there is an algorithm that always works. This algorithm is Gauss’s Method (or Gaussian elimination or linear elimination).

1.4 Example To solve this system

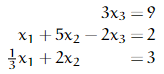
we transform it, step by step, until it is in a form that we can easily solve.

The first transformation rewrites the system by interchanging the first and third row.

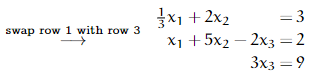
The second transformation rescales the first row by a factor of 3.

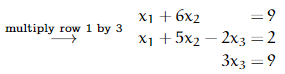
The third transformation is the only nontrivial one in this example. We mentally multiply both sides of the first row by −1, mentally add that to the second row, and write the result in as the new second row.

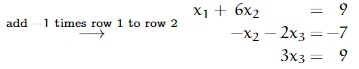
These steps have brought the system to a form where we can easily find the value of each variable. The bottom equation shows that x3 = 3. Substituting 3 for x3 in the middle equation shows that x2 = 1. Substituting those two into the top equation gives that x1 = 3. Thus the system has a unique solution; the solution set is {(3, 1, 3) }.

We will use Gauss’s Method throughout the book. It is fast and easy. We will now show that it is also safe: Gauss’s Method never loses solutions nor does it ever pick up extraneous solutions, so that a tuple is a solution to the system before we apply the method if and only if it is a solution after.