Linear Algebra

What is Linear Algebra?

Many difficult problems can be handled easily once relevant information is organized in a certain way. This text aims to teach you how to organize in- formation in cases where certain mathematical structures are present. Linear algebra is, in general, the study of those structures. Namely

Linear algebra is the study of vectors and linear functions.

In broad terms, vectors are things you can add and linear functions are functions of vectors that respect vector addition. The goal of this text is to teach you to organize information about vector spaces in a way that makes problems involving linear functions of many variables easy. (Or at least tractable.)

To get a feel for the general idea of organizing information, of vectors, and of linear functions this chapter has brief sections on each. We start here in hopes of putting students in the right mindset for the odyssey that follows; the latter chapters cover the same material at a slower pace. Please be prepared to change the way you think about some familiar mathematical objects and keep a pencil and piece of paper handy!

1.1 Organizing Information

Functions of several variables are often presented in one line such as f(x, y) = 3x+ 5y .

But lets think carefully; what is the left hand side of this equation doing? Functions and equations are different mathematical objects so why is the equal sign necessary?

A Sophisticated Review of Functions (Video)

If someone says

“Consider the function of two variables 7β − 13b.”

we do not quite have all the information we need to determine the relationship between inputs and outputs.

Example 1 (Of organizing and reorganizing information)

You own stock in 3 companies: Google, Netflix, and Apple. The value V of your stock portfolio as a function of the number of shares you own sN , sG, sA of these companies is

24sG + 80sA + 35sN .

Here is an ill posed question: what is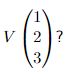

The column of three numbers is ambiguous! Is it is meant to denote

• 1 share of G, 2 shares of N and 3 shares of A?
• 1 share of N , 2 shares of G and 3 shares of A?

Do we multiply the first number of the input by 24 or by 35? No one has specified an order for the variables, so we do not know how to calculate an output associated with a particular input.

A different notation for V can clear this up; we can denote V itself as an ordered triple of numbers that reminds us what to do to each number from the input.

If we change the order for the variables we should change the notation for V .

The subscripts B and B′ on the columns of numbers are just symbols2 reminding us of how to interpret the column of numbers. But the distinction is critical; as shown above V assigns completely different numbers to the same columns of numbers with different subscripts.

There are six different ways to order the three companies. Each way will give different notation for the same function V , and a different way of assigning numbers to columns of three numbers. Thus, it is critical to make clear which ordering is used if the reader is to understand what is written. Doing so is a way of organizing information.

This example is a hint at a much bigger idea central to the text; our choice of order is an example of choosing a basis3.

The main lesson of an introductory linear algebra course is this: you have considerable freedom in how you organize information about certain functions, and you can use that freedom to

1. uncover aspects of functions that don’t change with the choice (Ch 12)
2. make calculations maximally easy (Ch 13 and Ch 17)
3. approximate functions of several variables (Ch 17).

Unfortunately, because the subject (at least for those learning it) requires seemingly arcane and tedious computations involving large arrays of numbers known as matrices, the key concepts and the wide applicability of linear algebra are easily missed. So we reiterate,

Linear algebra is the study of vectors and linear functions.

In broad terms, vectors are things you can add and linear functions are functions of vectors that respect vector addition.