Introduction to Real Analysis

Chapter 1 – The Real Numbers

1.1 The Real Number System

Having taken calculus, you know a lot about the real number system; however, you probably do not know that all its properties follow from a few basic ones. Although we will not carry out the development of the real number system from these basic properties, it is useful to state them as a starting point for the study of real analysis and also to focus on one property, completeness, that is probably new to you.

Field Properties

The real number system (which we will often call simply the reals) is first of all a set {a, b, c, ….} on which the operations of addition and multiplication are defined so that every pair of real numbers has a unique sum and product, both real numbers, with the following properties.

(A) a + b = b + a and ab = ba (commutative laws).
(B) (a + b)+ c = a + (b + c) and (ab)c = a(bc) (associative laws).
(C) a(b + c) = ab + ac (distributive law).
(D) There are distinct real numbers 0 and 1 such that a + 0 = a and a1 = a for all a.
(E) For each a there is a real number 1/a such that a + ( -a) = 0, and if , there is a real number 1=a such that a(1/a)=1

.

The manipulative properties of the real numbers, such as the relations

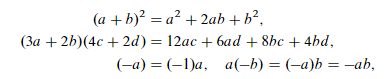
and

all follow from (A)–(E). We assume that you are familiar with these properties. A set on which two operations are defined so as to have properties (A)–(E) is called a

field. The real number system is by no means the only field. The rational numbers (which are the real numbers that can be written as r = p/q, where p and q are integers and a) also form a field under addition and multiplication. The simplest possible field consists of two elements, which we denote by 0 and 1, with addition defined by

0+ 0 = 1 + 1 = 0 , 1 + 0 = 0 + 1 = 1

and multiplication defined by

0 . 0 = 0 . 1 = 1 . 0 = 0 , 1 . 1 = 1