How We Got From There To Here: A Story of Real Analysis

Prologue: Three Lessons Before We Begin

2.1 Lesson One

Get a pad of paper and write down the answer to this question: What is . . . No, really. We’re serious. Get a writing pad. We’ll wait.

We really are serious about this. Get a pad of paper!

Got it? Good. Now write down your answer to this question: What is a number? Don’t think about it. Don’t analyze it. Don’t consider it. Just write down the best answer you can without thinking. You are the only person who ever needs to see what you’ve written.

Done? Good.

Now consider this: All of the objects listed below are “numbers” in a sense we will not make explicit here. How many of them does your definition include?

• 1
• −1
• 0
• 3/5
• √
• 2
• √ −1
• ii
• e5i
• 4 + 3i− 2j + 6k (this is called a quaternion)
• dx (this is the differential you learned all about in calculus)
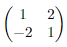•  (yes, matrices can be considered numbers).

Surely you included 1. Almost surely you included 3/5. But what about 0? −1? Does your definition include √ 2? Do you consider dx a number? Leibniz did. Any of the others? (And, yes, they really are all “numbers.”)

The lesson in this little demonstration is this: You don’t really have a clear notion of what we mean when we use the word “number.” And this is fine. Not knowing is acceptable.

Sometimes it is even encouraged.

A principal goal of this course of study is to rectify this, at least a little bit. When the course is over you may or may not be able to give a better definition of the word “number” but you will have a deeper understanding of the real numbers at least. That is enough for now.

2.2 Lesson Two

Read and understand the following development of the Quadratic Formula.

Suppose a  0. If  (.1)

then (.2)

Now let  giving

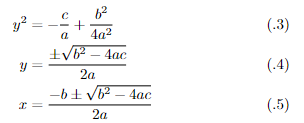
Were you able to follow the argument? Probably the step from equation (.1) to equation (.2) presented no difficulties. But what about the next step? Do you see where equation (.3) came from? If so, good for you. Most students, in fact most mathematicians, cannot make that step in their heads. But are you sure? Is there, perhaps, some small detail you’ve overlooked?

Check to see.

That is, let x = y − b/ 2a in equation (.2) and see if you can get equation (.3). Do it on that handy pad of paper we told you to get out earlier. Do it now. We’ll wait.

If you still haven’t gotten out a pad of paper, give up now. You’re going to fail this course. Seriously. Do you think we would spend so much time on this, that we would repeat it so many times, if it weren’t important. GET OUT A PAD OF PAPER NOW! Last chance. You’ve been warned.

Done? Good.

Perhaps you haven’t been able to fill in the details on your own. That’s ok. Many people can’t. If not then get help: from a classmate, a friend, your instructor, whomever. Unfortunately most people won’t get help in this situation. Instead they will perceive this as “failure,” hide it and berate themselves or the problem as “stupid.” In short they will let their personal insecurities and demons overwhelm them. Don’t do this. Get help. You are neither dumb nor incapable. There are a thousand reasons that on any given day you might not be able to solve this problem. But don’t let a bad day interfere with the education you are here for. Get someone to help you over this hump. Later you will be able to help your helper in the same way. Really.

At this point we assume that you’ve successfully negotiated the transition from equation (.2) to equation (.5).

See? It really wasn’t that bad after all. Just a lot of elementary algebra. Now that you’ve done it (or seen it done), it is easy to see that there really wasn’t much there.

But this is the point! We left those computations out precisely because we knew that they were routine and that you could fill in the details. Moreover, filling in the details yourself gives you a little better insight into the computations. If we’d filled them in for you we would have robbed you of that insight. And we would have made this book longer than it needs to be. We don’t want to do either of those things. If we fill in all of the details of every computation for you, you won’t learn to have confidence in your ability to do them yourself. And this book will easily double in length.

So the lesson here is this: Keep that pad of paper handy whenever you are reading this (or any other) mathematics text. You will need it. Routine computations will often be skipped. But calling them “routine” and skipping them does not mean that they are unimportant. If they were truly unimportant we would leave them out entirely.

Moreover “routine” does not mean “obvious.” Every step we took in the development of the Quadratic Formula was “routine.” But even routine computations need to be understood and the best way to understand them is to do them. This is the way to learn mathematics; it is the only way that really works. Don’t deprive yourself of your mathematics education by skipping the most important parts. If you didn’t fill in those details you’re being stupid (or at least unduly stubborn). There is a good reason for putting these three lessons first. Stop wasting your time and intellect! Go do it now.

As you saw when you filled in the details of our development of the Quadratic Formula the substitution x = y − b

2a was crucial because it turned

into

where k depends only on a, b, and c. In the sixteenth century a similar technique was used by Ludovico Ferrari (1522-1565) to reduce the general cubic equation

into the so-called “depressed cubic”

where p, and q depend only on a, b, c, and d.

The general depressed cubic had previously been solved by Tartaglia (the Stutterer, 1500-1557) so converting the general cubic into a depressed cubic provided a path for Ferrari to compute the “Cubic Formula” — like the Quadratic Formula but better.

It is not entirely clear why eliminating the quadratic term should be depressing, but there it is.