Discrete Structures for Computer Science – Counting, Recursion, and Probability

Chapter 1 – Introduction

In this chapter, we introduce some problems that will be solved later in this book. Along the way, we recall some notions from discrete mathematics that you are assumed to be familiar with. These notions are reviewed in more detail in Chapter 2.

1.1 Ramsey Theory

Ramsey Theory studies problems of the following form: How many elements of a given type must there be so that we can guarantee that some property holds? In this section, we consider the case when the elements are people and the property is “there is a large group of friends or there is a large group of strangers”.

Theorem 1.1.1 In any group of six people, there are

• three friends, i.e., three people who know each other,
• or three strangers, i.e., three people, none of which knows the other two.

In order to prove this theorem, we denote the six people by P1, P2, . . . , P6. Any two people Pi and Pj are either friends or strangers. We define the complete graph G = (V,E) with vertex set

V = {Pi : 1 ≤ i ≤ 6}

and edge set

E = {PiPj : 1 ≤ i < j ≤ 6}.

Observe that |V | = 6 and |E| = 15. We draw each edge PiPj as a straight-line segment according to the following rule:

• If Pi and Pj are friends, then the edge PiPj is drawn as a solid segment.
• If Pi and Pj are strangers, then the edge PiPj is drawn as a dashed segment.

In the example below, P3 and P5 are friends, whereas P1 and P3 are strangers.

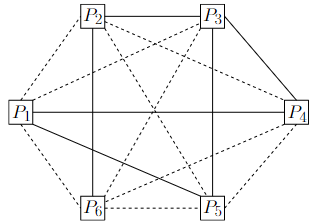
Observe that a group of three friends corresponds to a solid triangle in the graph G, whereas a group of three strangers corresponds to a dashed triangle. In the example above, there is no solid triangle and, thus, there is no group of three friends. Since the triangle P2P4P5 is dashed, there is a group of three strangers.

Using this terminology, Theorem 1.1.1 is equivalent to the following:

Theorem 1.1.2 Consider a complete graph on six vertices, in which each edge is either solid or dashed. Then there is a solid triangle or a dashed triangle.

Proof. As before, we denote the vertices by P1, . . . , P6. Consider the five edges that are incident on P1. Using a proof by contradiction, it can easily be shown that one of the following two claims must hold:

• At least three of these five edges are solid.
• At least three of these five edges are dashed.

We may assume, without loss of generality, that the first claim holds. (Do you see why?) Consider three edges incident on P1 that are solid and denote them by P1A, P1B, and P1C.

If at least one of the edges AB, AC, and BC is solid, then there is a solid triangle. In the left figure below, AB is solid and we obtain the solid triangle P1AB.

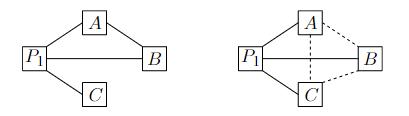
Otherwise, all edges AB, AC, and BC are dashed, in which case we obtain the dashed triangle ABC; see the right figure above.

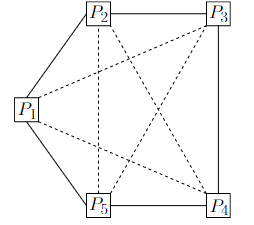
You should convince yourself that Theorem 1.1.2 also holds for complete graphs with more than six vertices. The example below shows an example of a complete graph with five vertices without any solid triangle and without any dashed triangle. Thus, Theorem 1.1.2 does not hold for complete graphs with five vertices. Equivalently, Theorem 1.1.1 does not hold for groups of five people.

What about larger groups of friends/strangers? Let k ≥ 3 be an integer. The following theorem states that even if we take b2k/2c people, we are not guaranteed that there is a group of k friends or a group of k strangers.

A k-clique in a graph is a set of k vertices, any two of which are connected by an edge. For example, a 3-clique is a triangle.

Theorem 1.1.3 Let k ≥ 3 and n ≥ 3 be integers with n ≤ b2k/2c. There exists a complete graph with n vertices, in which each edge is either solid or dashed, such that this graph does not contain a solid k-clique and does not contain a dashed k-clique.

We will prove this theorem in Section 7.2, using elementary counting techniques and probability theory. This probably sounds surprising to you, because Theorem 1.1.3 does not have anything to do with probability. In fact, in Section 7.2, we will prove the following claim: Take k = 20 and n = 1024. If you go to the ByWard Market in downtown Ottawa and take a random group of n people, then with very high probability, this group does not contain a subgroup of k friends and does not contain a subgroup of k strangers. In other words, with very high probability, every subgroup of k people contains two friends and two strangers.