Category Theory for Scientists

Chapter 1 – Introduction

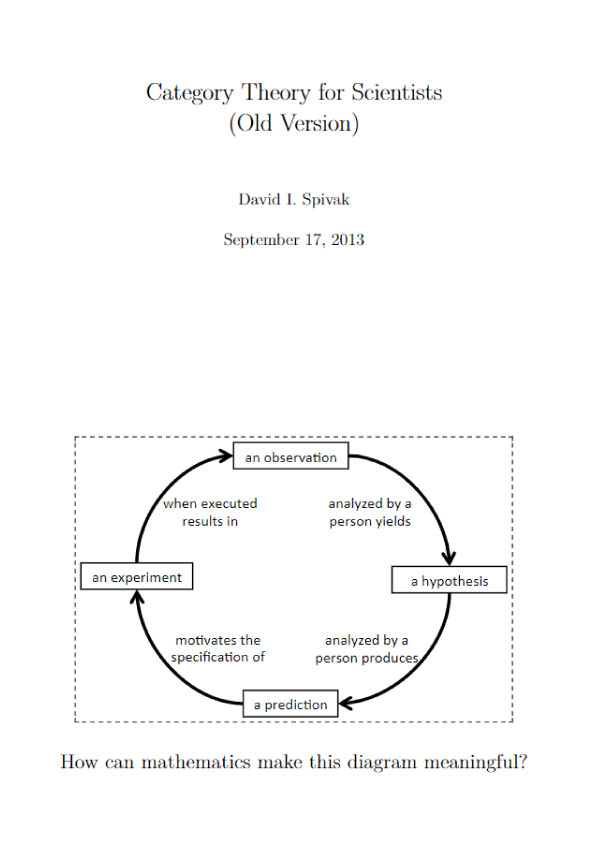
The title page of this book contains a graphic that we reproduce here.

It is intended to evoke thoughts of the scientific method.

A hypothesis analyzed by a person produces a prediction, which motivates the specification of an experiment, which when executed results in an observation, which analyzed by a person yields a hypothesis.

This sounds valid, and a good graphic can be exceptionally useful for leading a reader through the story that the author wishes to tell.

Interestingly, a graphic has the power to evoke feelings of understanding, without really meaning much. The same is true for text: it is possible to use a language such as English to express ideas that are never made rigorous or clear. When someone says “I believe in free will,” what does she believe in? We may all have some concept of what she’s saying—something we can conceptually work with and discuss or argue about. But to what extent are we all discussing the same thing, the thing she intended to convey?

Science is about agreement. When we supply a convincing argument, the result of this convincing is agreement. When, in an experiment, the observation matches the hypothesis—success!—that is agreement. When my methods make sense to you, that is agreement. When practice does not agree with theory, that is disagreement. Agreement is the good stuff in science; it’s the high fives.

But it is easy to think we’re in agreement, when really we’re not. Modeling our thoughts on heuristics and pictures may be convenient for quick travel down the road, but we’re liable to miss our turnoff at the first mile. The danger is in mistaking our convenient conceptualizations for what’s actually there. It is imperative that we have the ability at any time to ground out in reality. What does that mean?

Data. Hard evidence. The physical world. It is here that science touches down and heuristics evaporate. So let’s look again at the diagram on the cover. It is intended to evoke an idea of how science is performed. Is there hard evidence and data to back this theory up? Can we set up an experiment to find out whether science is actually performed according to such a protocol? To do so we have to shake off the stupor evoked by the diagram and ask the question: “what does this diagram intend to communicate?”

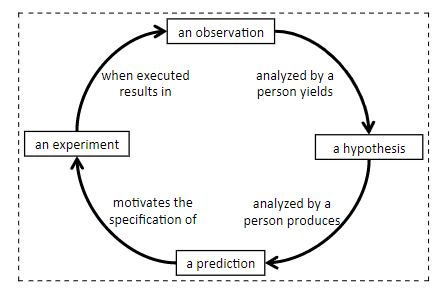
In this course I will use a mathematical tool called ologs, or ontology logs, to give some structure to the kinds of ideas that are often communicated in pictures like the one on the cover. Each olog inherently offers a framework in which to record data about the subject. More precisely it encompasses a database schema, which means a system of interconnected tables that are initially empty but into which data can be entered. For example consider the olog below

(1.1)

This olog represents a framework in which to record data about objects held above the ground, their mass, their height, and a comparison (the ?-mark in the middle) between the number of seconds till they hit the ground and a certain real-valued function of their height. We will discuss ologs in detail throughout this course.

The picture in (1.1) looks like an olog, but it does not conform to the rules that we lay out for ologs in Section 2.3. In an olog, every arrow is intended to represent a mathematical function. It is difficult to imagine a function that takes in predictions and outputs experiments, but such a function is necessary in order for the arrow

in (1.1) to make sense. To produce an experiment design from a prediction probably requires an expert, and even then the expert may be motivated to specify a different experiment on Tuesday than he is on Monday. But perhaps our criticism has led to a way forward: if we say that every arrow represents a function when in the context of a specific expert who is actually doing the science at a specific time, then Figure (1.1) begins to make sense. In fact, we will return to the figure in Section 5.3 (specifically Example 5.3.3.10), where background methodological context is discussed in earnest.

This course is an attempt to extol the virtues of a new branch of mathematics, called category theory, which was invented for powerful communication of ideas between different fields and subfields within mathematics. By powerful communication of ideas I actually mean something precise. Different branches of mathematics can be formalized into categories. These categories can then be connected together by functors. And the sense in which these functors provide powerful communication of ideas is that facts and theorems proven in one category can be transferred through a connecting functor to yield proofs of analogous theorems in another category. A functor is like a conductor of mathematical truth.

I believe that the language and toolset of category theory can be useful throughout science. We build scientific understanding by developing models, and category theory is the study of basic conceptual building blocks and how they cleanly fit together to make such models. Certain structures and conceptual frameworks show up again and again in our understanding of reality. No one would dispute that vector spaces are ubiquitous. But so are hierarchies, symmetries, actions of agents on objects, data models, global behavior emerging as the aggregate of local behavior, self-similarity, and the effect of methodological context.

Some ideas are so common that our use of them goes virtually undetected, such as set- theoretic intersections. For example, when we speak of a material that is both lightweight and ductile, we are intersecting two sets. But what is the use of even mentioning this set-theoretic fact? The answer is that when we formalize our ideas, our understanding is almost always clarified. Our ability to communicate with others is enhanced, and the possibility for developing new insights expands. And if we are ever to get to the point that we can input our ideas into computers, we will need to be able to formalize these ideas first.

It is my hope that this course will offer scientists a new vocabulary in which to think and communicate, and a new pipeline to the vast array of theorems that exist and are considered immensely powerful within mathematics. These theorems have not made their way out into the world of science, but they are directly applicable there. Hierarchies are partial orders, symmetries are group elements, data models are categories, agent actions are monoid actions, local-to-global principles are sheaves, self-similarity is modeled by operads, context can be modeled by monads.