Category Theory for Programmers

Category: The Essence of Composition

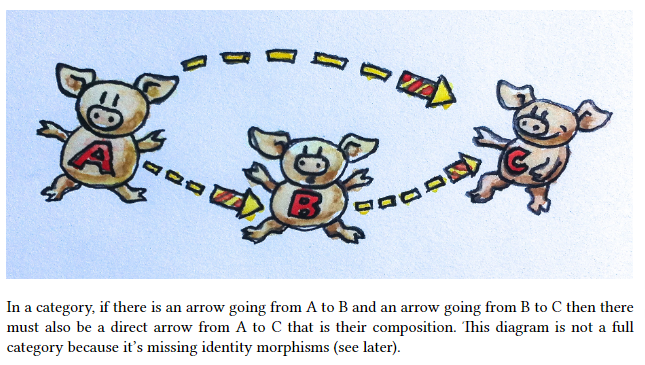
A category is an embarrassingly simple concept. A category consists of objects and arrows that go between them. That’s why categories are so easy to represent pictorially. An object can be drawn as a circle or a point, and an arrow… is an arrow. (Just for variety, I will occasionally draw objects as piggies and arrows as fireworks.) But the essence of a category is composition. Or, if you prefer, the essence of composition is a category. Arrows compose, so if you have an arrow from object A to object B, and another arrow from object B to object C, then there must be an arrow — their composition — that goes from A to C.

1.1 Arrows as Functions

Is this already too much abstract nonsense? Do not despair. Let’s talk concretes. Think of arrows, which are also called morphisms, as functions. You have a function f that takes an argument of type A and returns a B. You have another function g that takes a B and returns a C. You can compose them by passing the result of f to g. You have just defined a new function that takes an A and returns a C.

In math, such composition is denoted by a small circle between functions: 𝑔 ∘ 𝑓 . Notice the right to left order of composition. For some people this is confusing. You may be familiar with the pipe notation in Unix, as in:

lsof | grep Chrome

or the chevron >> in F#, which both go from left to right. But in mathematics and in Haskell functions compose right to left. It helps if you read g◦f as “g after f.”

Let’s make this even more explicit by writing some C code. We have one function f that takes an argument of type A and returns a value of type B:

B f(A a);

and another:

C g(B b);

Their composition is:

C g_after_f(A a)
{
return g(f(a));
}

Here, again, you see right-to-left composition: g(f(a)); this time in C.

I wish I could tell you that there is a template in the C++ Standard Library that takes two functions and returns their composition, but there isn’t one. So let’s try some Haskell for a change. Here’s the declaration of a function from A to B:

f :: A -> B

Similarly:

g :: B -> C

Their composition is:

g . f

Once you see how simple things are in Haskell, the inability to express straightforward functional concepts in C++ is a little embarrassing. In fact, Haskell will let you use Unicode characters so you can write com- position as:

g ◦ f

You can even use Unicode double colons and arrows:

f ∷ A → B

So here’s the first Haskell lesson: Double colon means “has the type of…” A function type is created by inserting an arrow between two types. You compose two functions by inserting a period between them (or a Unicode circle).