Read More: Calculus 1 & Calculus 3
5: Integration
We have spent considerable me considering the derivatives of a function and their applications. In the following chapters, we are going to star ng thinking in “the other direction.” That is, given a function f(x), we are going to consider functions F(x) such that F ′(x) = f(x). There are numerous reasons this will prove to be useful: these functions will help us compute area, volume, mass, force, pressure, work, and much more.
5.1 An derivatives and Indefinite Integration
Given a function y = f(x), a differential equation is one that incorporates y, x, and the derivatives of y. For instance, a simple differential equation is:
y ′ = 2x.
Solving a differential equation amounts to finding a function y that satisfies the given equation. Take a moment and consider that equation; can you find a function y such that y ′ = 2x?
Can you find another?
And yet another?
Hopefully one was able to come up with at least one solution: y = x2. “Finding another” may have seemed impossible un l one realizes that a function like y = x2 + 1 also has a derivative of 2x. Once that discovery is made, finding “yet another” is not difficult; the function y = x2 + 123, 456, 789 also has a derivative of 2x. The differential equation y ′ = 2x has many solutions. This leads us to some definitions.
Definition 5.1.1
An derivatives and Indefinite Integrals
Let a function f(x) be given. An an derivative of f(x) is a function F(x) such that F ′(x) = f(x).
The set of all an derivatives of f(x) is the indefinite integral of f, denoted by ∫ f(x) dx.
Make a note about our definition: we refer to an an derivative of f, as op- posed to the an derivative of f, since there is always an infinite number of them.
adding a constant. Not only does this give us more an derivatives, it gives us all of them.
Theorem 5.1.1
An derivative Forms
Let F(x) and G(x) be an derivatives of f(x) on an interval I. Then there exists a constant C such that, on I,
G(x) = F(x) + C.
Given a function f defined on an interval I and one of its an derivatives F, we know all an derivatives of f on I have the form F(x) + C for some constant C. Using Definition 5.1.1, we can say that
∫f(x) dx = F(x) + C.
Let’s analyze this indefinite integral nota on.
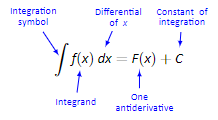
(Figure 5.1.1: Understanding the indefinite integral nota on)
Figure 5.1.1 shows the typical nota on of the indefinite integral. The integration symbol, ∫ , is in reality an “elongated S,” representing “take the sum.” We will later see how sums and an derivatives are related.
The function we want to find an an derivative of is called the integrand. It contains the differential of the variable we are integrating with respect to. The ∫ symbol and the differential dx are not “bookends” with a function sandwiched in between; rather, the symbol ∫ means “find all an derivatives of what follows,” and the function f(x) and dx are multiplied together; the dx does not “just sit there.”











