APEX Calculus 3

Read More: Calculus 1 & Calculus 2

9: Curves In The Plane

We have explored functions of the form y = f(x) closely throughout this text. We have explored their limits, their derivatives and their an derivatives; we have learned to identify key features of their graphs, such as relative maxima and minima, inflection points and asymptotes; we have found equations of their tangent lines, the areas between portions of their graphs and the x-axis, and the volumes of solids generated by revolving portions of their graphs about a horizontal or vertical axis.

Despite all this, the graphs created by functions of the form y = f(x) are limited. Since each x-value can correspond to only 1 y-value, common shapes like circles cannot be fully described by a function in this form. Fittingly, the “vertical line test” excludes vertical lines from being functions of x, even though these lines are important in mathematics.

In this chapter we’ll explore new ways of drawing curves in the plane. We’ll still work within the framework of functions, as an input will still only correspond to one output. However, our new techniques of drawing curves will render the vertical line test pointless, and allow us to create important – and beautiful – new curves. Once these curves are defined, we’ll apply the concepts of calculus to them, continuing to find equations of tangent lines and the areas of enclosed regions.

9.1 Conic Sections

The ancient Greeks recognized that interesting shapes can be formed by intersecting a plane with a double napped cone (i.e., two identical cones placed tip– to– tip as shown in the following figures). As these shapes are formed as sections of conics, they have earned the official name “conic sections.”

The three “most interesting” conic sections are given in the top row of Figure 9.1.1. They are the parabola, the ellipse (which includes circles) and the hyperbola. In each of these cases, the plane does not intersect the tips of the cones (usually taken to be the origin).

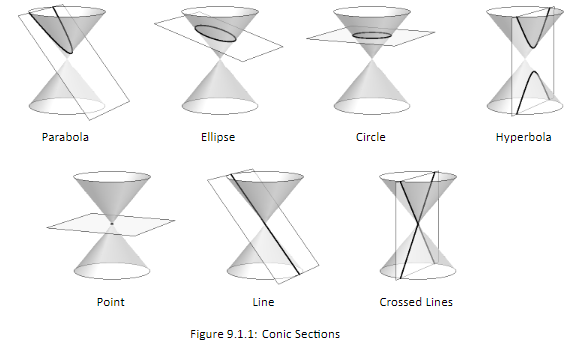
When the plane does contain the origin, three degenerate cones can be formed as shown the bottom row of Figure 9.1.1: a point, a line, and crossed lines. We focus here on the nondegenerate cases.

While the above geometric constructs define the conics in an intuitive, visual way, these constructs are not very helpful when trying to analyze the shapes algebraically or consider them as the graph of a function. It can be shown that all conics can be defined by the general second–degree equation

While this algebraic definition has its uses, most find another geometric perspective of the conics more beneficial.

Each nondegenerate conic can be defined as the locus, or set, of points that satisfy a certain distance property. These distance properties can be used to generate an algebraic formula, allowing us to study each conic as the graph of a function.