An Introduction to the Theory of Numbers

We consider problems concerning the number of ways in which a number can be written as a sum. If the order of the terms in the sum is taken into account the sum is called a composition and the number of compositions of n is denoted by c(n). If the order is not taken into account the sum is a partition and the number of partitions of n is denoted by p(n). Thus, the compositions of 3 are

3 = 3, 3 = 1 + 2, 3 = 2 + 1, and 3 = 1 + 1 + 1,

so that c(3) = 4. The partitions of 3 are

3 = 3, 3 = 2 + 1, and 3 = 1 + 1 + 1,

so p(3) = 3.

There are essentially three methods of obtaining results on compositions and partitions. First by purely combinatorial arguments, second by algebraic arguments with generating series, and finally by analytic operations on the generating series. We shall discuss only the first two of these methods.

We consider first compositions, these being easier to handle than partitions. The function c(n) is easily determined as follows. Consider n written as a sum of 1’s. We have n − 1 spaces between them and in each of the spaces we can insert a slash, yielding 2n−1 possibilities corresponding to the 2n−1 composition of n. For example

3 = 1 1 1, 3 = 1/1 1, 3 = 1 1/1, 3 = 1/1/1.

Just to illustrate the algebraic method in this rather trivial case we consider

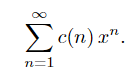
It is easily verified that

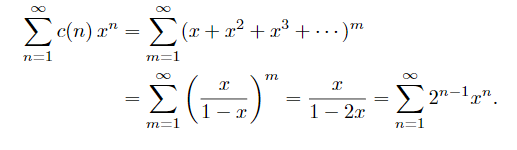
Examples. As an exercise I would suggest using both the combinatorial method and the algebraic approach to prove the following results:

1. The number of compositions of n into exactly m parts is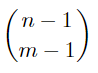(Catalan);
2. The number of compositions of n into even parts is 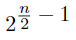if n is even and 0 if n is odd;
3. The number of compositions of n into an even number of parts is equal to the number of compositions of n into an odd number of parts.

Somewhat more interesting is the determination of the number of compositions of n into odd parts. Here the algebraic approach yields

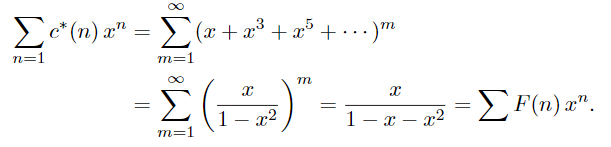
By cross multiplying the last two expressions we see that

Thus the F ’s are the so-called Fibonacci numbers

1, 1, 2, 3, 5, 8, 13, . . . .

The generating function yields two explicit expressions for these numbers. First, by “partial fractioning”  , expanding each term as a power series and comparing coefficients, we obtain

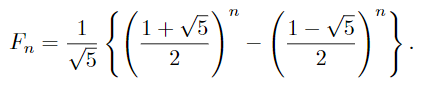
Another expression for is obtained by observing that x

Comparing the coefficients here we obtain (Lucas)

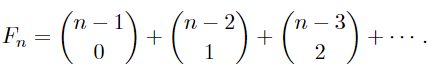
You might consider the problem of deducing this formula by combinatorial arguments.

Suppose we denote by a(n) the number of compositions of n with all summands at most 2, and by b(n) the number of compositions of n with all summands at least 2. An interesting result is that a(n) = b(n + 2). I shall prove this result and suggest the problem of finding a reasonable generalization.

First note that a(n) = a(n− 1) + a(n− 2). This follows from the fact that every admissible composition ends in 1 or 2. By deleting this last summand, we obtain an admissible composition of n − 1 and n − 2 respectively. Since a(1) = 1 and a(2) = 2, it follows that a(n) = Fn. The function b(n) satisfies the same recursion formula. In fact, if the last summand in an admissible composition of n is 2, delete it to obtain an admissible composition of n − 2; if the last summand is greater than 2, reduce it by 1 to obtain an admissible composition of n − 1. Since b(2) = b(3) = 1, it follows that so that .

An interesting idea for compositions is that of weight of a composition. Suppose we associate with each composition a number called the weight, which is the product of the summands. We shall determine the sum w(n) of the weights of the compositions of n. The generating function of w(n) is

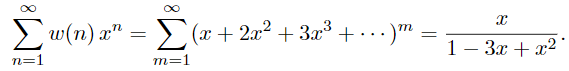
From this we find that . I leave it as an exercise to prove from this that .

We now turn to partitions. There is no simple explicit formula for p(n). Our main objective here will be to prove the recursion formula

discovered by Euler. The algebraic approach to partition theory depends on algebraic manipulations with the generating function

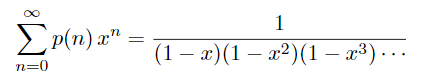
and related functions for restricted partitions. The combinatorial approach depends on the use of partition (Ferrer) diagrams.