Notes on Diffy Qs – Differential Equations for Engineers

Introduction to differential equations 

Note: more than 1 lecture, §1.1 in [EP], chapter 1 in [BD]

 Differential equations 

The laws of physics are generally written down as differential equations. Therefore, all of science and engineering use differential equations to some degree. Understanding differential equations is essential to understanding almost anything you will study in your science and engineering classes. You can think of mathematics as the language of science, and differential equations are one of the most important parts of this language as far as science and engineering are concerned. As an analogy, suppose all your classes from now on were given in Swahili. It would be important to first learn Swahili, or you would have a very tough time getting a good grade in your classes.

You saw many differential equations already without perhaps knowing about it. And you even solved simple differential equations when you took calculus. Let us see an example you may not have seen:

𝑑𝑥/𝑑𝑡 + 𝑥 = 2 cos 𝑡. (1)

Here 𝑥 is the dependent variable and 𝑡 is the independent variable. Equation (1) is a basic example of a differential equation. It is an example of a first order differential equation, since it involves only the first derivative of the dependent variable. This equation arises from Newton’s law of cooling where the ambient temperature oscillates with time.

0.2.2 Solutions of differential equations 

Solving the differential equation means finding 𝑥 in terms of 𝑡. That is, we want to find a function of 𝑡, which we call 𝑥, such that when we plug 𝑥, 𝑡, and 𝑑𝑥/𝑑𝑡 into (1), the equation holds; that is, the left hand side equals the right hand side. It is the same idea as it would be for a normal (algebraic) equation of just 𝑥 and 𝑡. We claim that

𝑥 = 𝑥(𝑡) = cos 𝑡 + sin 𝑡

is a solution. How do we check? We simply plug 𝑥 into equation (1)! First we need to compute 𝑑𝑥/𝑑𝑡 . We find that 𝑑𝑥/𝑑𝑡 = − sin 𝑡 + cos 𝑡. Now let us compute the left-hand side of (1).

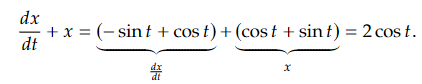
Yay! We got precisely the right-hand side. But there is more! We claim 𝑥 = cos 𝑡+ sin 𝑡+ 𝑒−𝑡 is also a solution. Let us try,

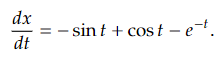
We plug into the left-hand side of (1) 𝑑𝑥 𝑑𝑡

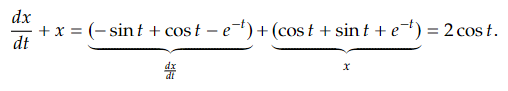
And it works yet again!

So there can be many different solutions. For this equation all solutions can be written in the form 𝑥 = cos 𝑡 + sin 𝑡 + 𝐶𝑒−𝑡 , for some constant 𝐶. Different constants 𝐶 will give different solutions, so there are really infinitely many possible solutions. See Figure 1 for the graph of a few of these solutions. We will see how we find these solutions a few lectures from now.

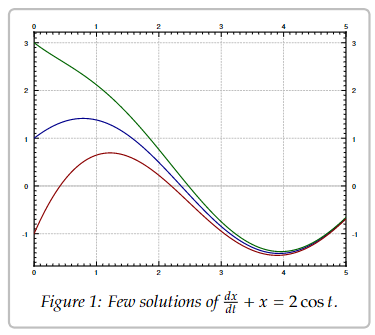
Figure 1: Few solutions of 𝑑𝑥/𝑑𝑡 + 𝑥 = 2 cos 𝑡.

Solving differential equations can be quite hard. There is no general method that solves every differential equation. We will generally focus on how to get exact for- mulas for solutions of certain differential equations, but we will also spend a little bit of time on getting approximate solutions. And we will spend some time on understanding the equations without solv- ing them.

Most of this book is dedicated to ordinary differential equations or ODEs, that is, equations with only one independent variable, where derivatives are only with respect to this one variable. If there are several independent variables, we get partial differential equations or PDEs.

Even for ODEs, which are very well understood, it is not a simple question of turning a crank to get answers. When you can find exact solutions, they are usually preferable to approximate solutions. It is important to understand how such solutions are found. Although in real applications you will leave much of the actual calculations to computers, you need to understand what they are doing. It is often necessary to simplify or transform your equations into something that a computer can understand and solve. You may even need to make certain assumptions and changes in your model to achieve this.

To be a successful engineer or scientist, you will be required to solve problems in your job that you never saw before. It is important to learn problem solving techniques, so that you may apply those techniques to new problems. A common mistake is to expect to learn some prescription for solving all the problems you will encounter in your later career. This course is no exception.