Combinatorics Through Guided Discovery

Chapter 1 – What is Combinatorics? 

Combinatorial mathematics arises from studying how we can combine objects into arrangements. For example, we might be combining sports teams into a tournament, samples of tires into plans to mount them on cars for testing, students into classes to compare approaches to teaching a subject, or members of a tennis club into pairs to play tennis. There are many questions one can ask about such arrangements of objects. Here we will focus on questions about how many ways we may combine the objects into arrangements of the desired type. These are called counting problems. Sometimes, though, combinatorial mathematicians ask if an arrangement is possible (if we have ten baseball teams, and each team has to play each other team once, can we schedule all the games if we only have the fields avail- able at enough times for forty games?). Sometimes they ask if all the arrangements we might be able to make have a certain desirable property (Do all ways of testing 5 brands of tires on 5 different cars [with certain additional properties] compare each brand with each other brand on at least one common car?). Problems of these sorts come up throughout physics, biology, computer science, statistics, and many other subjects. However, to demonstrate all these relationships, we would have to take detours into all these subjects. While we will give some important applications, we will usually phrase our discussions around everyday experience and mathematical experience so that the student does not have to learn a new context before learning mathematics in context!

1.1 About These Notes 

These notes are based on the philosophy that you learn the most about a subject when you are figuring it out directly for yourself, and learn the least when you are trying to figure out what someone else is saying about it. On the other hand, there is a subject called combinatorial mathematics, and that is what we are going to be studying, so we will have to tell you some basic facts. What we are going to try to do is to give you a chance to discover many of the interesting examples that usually appear as textbook examples and discover the principles that appear as textbook theorems. Your main activity will be solving problems designed to lead you to discover the basic principles of combinatorial mathematics. Some of the problems lead you through a new idea, some give you a chance to describe what you have

learned in a sequence of problems, and some are quite challenging. When you find a problem challenging, don’t give up on it, but don’t let it stop you from going on with other problems. Frequently you will find an idea in a later problem that you can take back to the one you skipped over or only partly finished in order to finish it off. With that in mind, let’s get started. In the problems that follow, you will see some problems marked on the left with various symbols. The preface gives a full explanation of these symbols and discusses in greater detail why the book is organized as it is! Table 1.1.1, which is repeated from the preface, summarizes the meaning of the symbols.

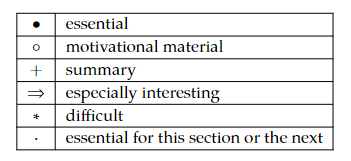
Table 1.1.1: The meaning of the symbols to the left of problem numbers.