![Free eBooks of IT [BooksOfAll]](https://www.booksofall.com/wp-content/uploads/2022/06/booksofall-logo-2.png){kind=logo}
Chapter 1 – Vectors and Geometry in Two and Three Dimensions
Before we get started doing calculus in two and three dimensions we need to brush up on some basic geometry, that we will use a lot. We are already familiar with the Cartesian plane, but we’ll start from the beginning.
1.1 Points
Each point in two dimensions may be labeled by two coordinates1(x, y) which specify the position of the point in some units with respect to some axes as in the figure below.
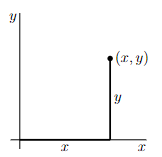
The set of all points in two dimensions is denoted2 R2. Observe that
- the distance from the point (x, y) to the x-axis is |y|
- if y > 0, then (x, y) is above the x-axis and if y < 0, then (x, y) is below the x-axis
- the distance from the point (x, y) to the y-axis is |x|
- if x > 0, then (x, y) is to the right of the y-axis and if x < 0, then (x, y) is to the left of the y-axis
- the distance from the point (x, y) to the origin (0, 0) is √ x2 + y2
Similarly, each point in three dimensions may be labeled by three coordinates (x, y, z), as in the two figures below.
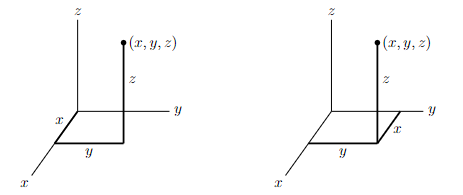
The set of all points in three dimensions is denoted R3. The plane that contains, for example, the x– and y-axes is called the xy-plane.
- The xy-plane is the set of all points (x, y, z) that satisfy z = 0.
- The xz-plane is the set of all points (x, y, z) that satisfy y = 0.
- The yz-plane is the set of all points (x, y, z) that satisfy x = 0.
More generally,
- The set of all points (x, y, z) that obey z = c is a plane that is parallel to the xy-plane and is a distance |c| from it. If c > 0, the plane z = c is above the xy-plane. If c < 0, the plane z = c is below the xy-plane. We say that the plane z = c is a signed distance c from the xy-plane.
- The set of all points (x, y, z) that obey y = b is a plane that is parallel to the xz-plane and is a signed distance b from it.
- The set of all points (x, y, z) that obey x = a is a plane that is parallel to the yz-plane and is a signed distance a from it.
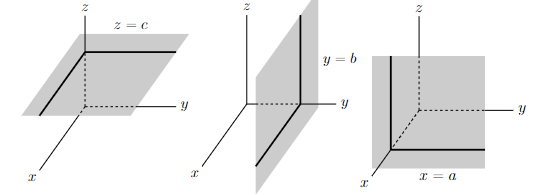
- Observe that our 2d distances extend quite easily to 3d.
- the distance from the point (x, y, z) to the xy-plane is |z|
- the distance from the point (x, y, z) to the xz-plane is |y|
- the distance from the point (x, y, z) to the yz-plane is |x|
- the distance from the point (x, y, z) to the origin (0, 0, 0) is
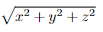
To see that the distance from the point (x, y, z) to the origin (0, 0, 0) is indeed√ x2 + y2 + z2,
- apply Pythagoras to the right-angled triangle with vertices (0, 0, 0), (x, 0, 0) and (x, y, 0) to see that the distance from (0, 0, 0) to (x, y, 0) is √ x2 + y2 and then
- apply Pythagoras to the right-angled triangle with vertices (0, 0, 0), (x, y, 0) and (x, y, z) to see that the distance from (0, 0, 0) to (x, y, z) is
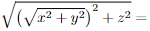
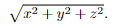
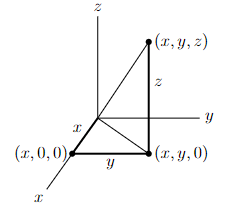
More generally, the distance from the point (x, y, z) to the point (x′, y′, z′) is 
.
Notice that this gives us the equation for a sphere quite directly. All the points on a sphere are equidistant from the centre of the sphere. So, for example, the equation of the sphere centered on (1, 2, 3) with radius 4, that is, the set of all points (x, y, z) whose distance from (1, 2, 3) is 4, is
