Chapter 1 – Integration
Calculus is built on two operations — differentiation and integration.
- Differentiation — as we saw last term, differentiation allows us to compute and study the instantaneous rate of change of quantities. At its most basic it allows us to compute tangent lines and velocities, but it also led us to quite sophisticated applications including approximation of functions through Taylor polynomials and optimisation of quantities by studying critical and singular points.
- Integration — at its most basic, allows us to analyse the area under a curve. Of course, its application and importance extend far beyond areas and it plays a central role in solving differential equations.
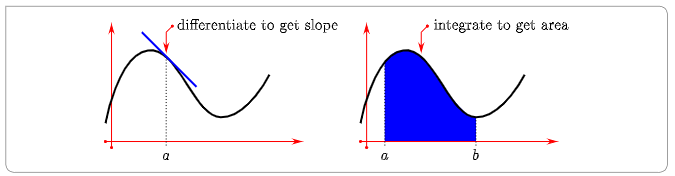
It is not immediately obvious that these two topics are related to each other. How- ever, as we shall see, they are indeed intimately linked.
1.1 Definition of the Integral
Arguably the easiest way to introduce integration is by considering the area between the graph of a given function and the x-axis, between two specific vertical lines — such as is shown in the figure above. We’ll follow this route by starting with a motivating example.
1.1.1 A Motivating Example
Let us find the area under the curve y = ex (and above the x-axis) for 0 ≤ x ≤ 1. That is, the area of { (x, y) ∣ 0 ≤ y ≤ ex, 0 ≤ x ≤ 1 } .
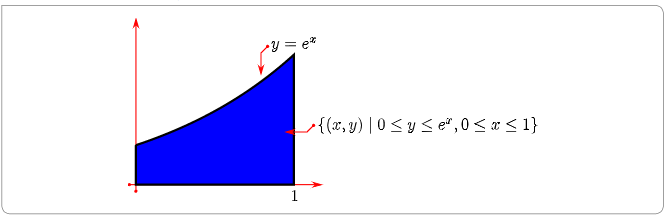
This area is equal to the “definite integral”
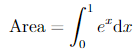
Do not worry about this notation or terminology just yet. We discuss it at length below. In different applications this quantity will have different interpretations — not just area. For example, if x is time and ex is your velocity at time x, then we’ll see later (in Example 1.1.18) that the specified area is the net distance travelled between time 0 and time 1. After we finish with the example, we’ll mimic it to give a general definition of the integral ∫ b a f(x)dx.